Двадесет и пет години по-късно един математик най-накрая разреши досадния „проблем с дивана“, за да помогне на Рос да пренесе новия си диван в апартамента си в"Приятели". Математическият проблем очертава дивана с най-голям размер, който може да се побере около ъгъл с дадена ширина - точно проблемът, пред който са изправени героите в епизод на "Приятели", излъчен през 1999 г.
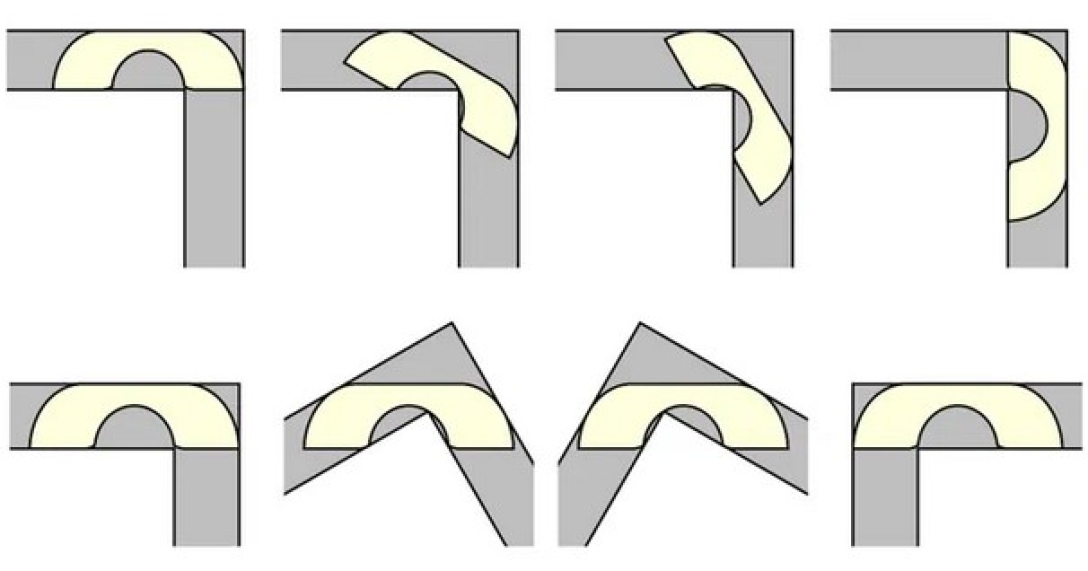
В математиката има много, на пръв поглед, необичайни задачи. Сред тях се откроява проблемът с преместването на диван, появил се за първи път през 1966 г. Това е математическа задача, която е двуизмерна симулация на реален ежедневен проблем с преместване на диван в апартамент или къща. Проблемът е да се намери двуизмерна форма на диван с максимална площ, която може да се движи през L-образен коридор, всяка част от който има дадена ширина за единица измерване и се събира под прав ъгъл.
Стойността на максималната площ на дивана се нарича "константа на дивана". Сега математик от Южна Корея намери решение на този проблем и публикува резултатите си на сървъра за предпечат ArXiv, пише Live Science.
Проблемът с преместването на дивана описва най-големия диван, който може да се побере в коридор, състоящ се от две части, които се срещат под прав ъгъл. Всъщност в реалния живот преместването на обикновен диван в такъв коридор би било изключително трудно, но тази задача предвижда необичайна форма на дивана, която позволява това да се направи.
Проблемът за преместването на диван е формулиран през 1966 г. от канадския математик Лео Мозер. Той предложи да се намери възможно най-голямата площ на една фигура в една равнина, която може да се движи около десния ъгъл на коридор с дадена ширина на единица измерване. Това е доста трудно, тъй като задачата включва както изчисляване на максималната площ, така и движението на фигурата.
Сега Джинеон Бек от университета Yensei в Южна Корея намери решение на този проблем. Той представи повече от 100 страници математически доказателства в своето изследване. Математикът откри, че за коридор с ширина 1 единица максималната площ на един въображаем диван може да бъде 2,2195 единици. Тоест това е самата „константа на дивана“. Така математикът представи по-точно решение на задачата, която преди беше в диапазона от 2,2195 до 2,37 единици. Това решение на проблема с преместването на дивана все още не е рецензирано от научната общност, тъй като други учени трябва да потвърдят, че това е оптималното решение.
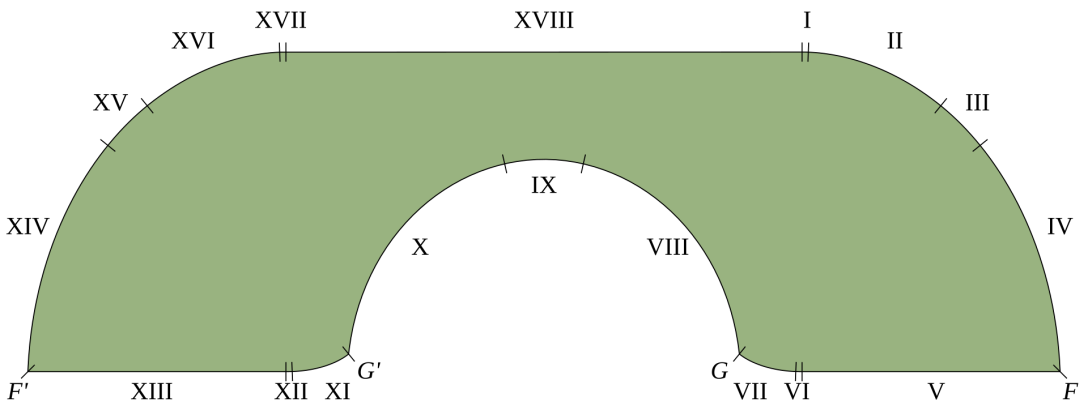
Така нареченият "диван на Гервер" е широк диван, който прилича малко на буквата U, има извита седалка и може да се мести L-образно в коридора, без да се заклещва. Въпросът беше дали този диван, направен от 18 отделни криви, съединени заедно, наистина има най-голямата и най-оптималната форма за движение по коридор под прав ъгъл по такъв начин, че да направи обратен завой. Бек разработи геометрията на формата на този диван и неговото движение и установи, че решението на Gerver е по същество правилно.
Прочетете още
- 16:59 „Ще дойдете ли с нас на бала?" Ученици трогнаха свой учител с уникална покана СНИМКИ
- 17:28 Нетаняху подозира Тръмп в заговор с Иран зад гърба на Израел
- 14:56 ГДБОП разби престъпна банда! Задържаха 8 души, иззеха пари и лъскави коли СНИМКИ
- 16:12 Жената на Васил Костадинов брани имиджа му с класифицирана информация